LA ESTABILIDAD COMO GARANTE DE LA SEGURIDAD DE LA VIDA EN EL MAR

  LOS CAMBIOS QUE PROVOCARON NAUFRAGIOS

 Las investigaciones de accidentes como el del 'O Bahía' o el 'Siempre Casina' determinan que la modificación de la estructura del buque o la mala distribución de los pesos causaron el siniestro

manuel barral | a coruña 24.11.2009 | 01:34

 Ver gráfico

          

La pérdida de estabilidad es la causa principal de los naufragios de los pesqueros. Las condiciones meteorológicas y el estado del mar pueden provocar esa falta de flotabilidad pero en muchos casos son las modificaciones en la estructura de los buques o la mala distribución de los pesos a bordo las que acaban por hacer zozobrar las embarcaciones. Es el caso de buques gallegos como el 'O Bahía' o el 'Siempre Casina', según recogen los informes de la investigación de estos accidentes publicados por el Ministerio de Fomento. La acción humana tuvo parte de culpa en dos siniestros en los que fallecieron un total de 18 marineros.

Las modificaciones estructurales de los pesqueros o la incorrecta distribución de pesos a bordo son algunos de los factores que, según los expertos, han provocado múltiples naufragios en las costas gallegas en los últimos años. Hasta ahora esta afirmación se basaba en el análisis que hacían ingenieros navales y otros profesionales sin una investigación a fondo de los sucesos pero desde ayer se puede comprobar que están en lo cierto. El Ministerio de Fomento publicó ayer los informes oficiales sobre accidentes marítimos elaborados por la Comisión Permanente de Investigación de Siniestros Marítimos desde el año 2000 hasta 2008 -año de su disolución- en los que se comprueba que en naufragios como el del pesquero O Bahía en junio de 2004 o el Siempre Casina en febrero de 2005 la mala distribución de pesos o cambios en la estructura de las embarcaciones provocaron una mayor inestabilidad y el hundimiento de las mismas. 

El organismo dependiente del Ministerio de Fomento realizó entre 2000 y 2008 casi 40 investigaciones de siniestros marítimos, desde accidentes de motos náuticas hasta choques de embarcaciones pasando por naufragios de buques de pesca o mercantes como el petrolero Prestige, pero los resultados no eran públicos a pesar de las numerosas solicitudes realizadas en este sentido desde distintos ámbitos marítimos. La publicación ahora de los informes responde a la intención de la nueva Comisión Permanente de Investigación de Accidentes e Incidentes Marítimos de dar una mayor transparencia a su actividad y que los resultados tengan valor pedagógico para todos los profesionales vinculados al mar. 

En esos ocho años los expertos de la comisión estudiaron los hechos que rodearon los naufragios de cuatro pesqueros con base en Galicia: el O Bahía, el Siempre Casina, el Sombriza y el Cordero, todos ellos con algún fallecido entre sus tripulantes: 

. 'O Bahía'. El cerquero con puerto base en Vigo naufragó el 2 de junio de 2004 frente a las islas Sisargas con el resultado de seis marineros muertos y cuatro desaparecidos. Según el informe de la comisión designada por Fomento, el pesquero se hundió por un vuelco tras perder la estabilidad. Entre los factores que provocaron el suceso, se señala el siguiente: "La existencia y disposición a bordo de pesos que, no habiendo sido considerados en el libro de estabilidad, se ha constatado que perjudicaron gravemente a la estabilidad del buque". El informe indica también que la velocidad "inadecuada" del barco ante unas condiciones de mar y viento adversas y la entrada de agua en sucesivas ocasiones "al no estar cerradas determinadas puertas y portillos en la superestructura y en el casco" favorecieron el siniestro de la embarcación. 
 

. 'Siempre Casina'. El naufragio de este pesquero se produjo el 22 de febrero de 2005 en la costa de Ribadeo y se saldó con seis marineros muertos, dos desaparecidos y uno rescatado. Al igual que en el caso del O Bahía, la Comisión Permanente de Investigación de Siniestros Marítimos apunta como principal causa del suceso la falta de estabilidad producida "por los efectos de la inundación de los parques de pesca y de los espacios situados bajo la cubierta principal del buque" pero aclara que "el embarque de agua se vio favorecido por el aumento de calado debido al incremento del peso en rosca causado por las modificaciones realizadas en la disposición general del buque". Estos cambios provocaron un aumento del peso de 9,3 toneladas -un 12,7% sobre el original- y que su centro de gravedad se elevase 16,2 centímetros. El informe descarta otras posibilidades del naufragio como una vía de agua, el abordaje o golpe con objetos a flote o sumergidos o la posible acción de cetáceos de grandes dimensiones y peso pues la inspección del casco del buque reveló que "estaba intacto, sin que se apreciaran grietas, abolladuras o signos de impacto". 
 

. 'Sombriza'. Esta pequeña embarcación matriculada en Viveiro se hundió el 7 de enero de 2008 frente a la costa de O Vicedo cuando sus dos tripulantes se disponían a calar las nasas entre Punta Chirlateira y Punta Camedo. Como consecuencia del hundimiento fallecieron los dos marineros de la embarcación. La investigación del incidente determina que el buque naufragó como consecuencia de una vía de agua aunque no ha podido establecer qué elemento ocasionó el impacto que perforó el forro del barco. Las condiciones en el momento del siniestro no eran adversas pero, a pesar de que la embarcación cumplía con las condiciones de seguridad marítima exigidas, no se hizo uso del equipo de VHF ni del material de salvamento que llevaba a bordo. 

. 'Cordero'. El arrastrero ribeirense zozobró el 15 de enero de 2008 frente a Cabo Prior y en el siniestro murió un tripulante, cuatro fueron dados por desaparecidos y tres pudieron ser rescatados. Según el informe de la comisión del Ministerio de Fomento que investigó el incidente, la inundación progresiva de los espacios interiores del pesquero, al registrarse una entrada de agua en el parque de pesca proveniente del sistema de baldeo, provocó su hundimiento. El informe aclara que las bombas destinadas a achicar el agua no pudieron cumplir su objetivo "bien por fallos en su funcionamiento o por falta de capacidad". El resultado de la investigación también concluye que, como explicó LA OPINIÓN tras el naufragio, el GPS de la radiobaliza no funcionó correctamente y que los pesqueros no mantuvieron la escucha obligatoria del canal 16 de VHF. Además, en la actuación de los marineros ante la emergencia, no pudieron zafar una de las balsas salvavidas "a pesar de intentarlo" y un chaleco salvavidas no se infló correctamente. 

La publicación de los informes de accidentes marítimos es uno de los cambios propuestos por la nueva Comisión Permanente de Investigación de Accidentes e Incidentes Marítimos que, desde el año pasado, ya no depende de Marina Mercante aunque sigue vinculada al Ministerio de Fomento. 

Los responsables de las investigaciones esperan sacar en los próximos meses las conclusiones de accidentes como el del Hermanos Landrove, el pasado 8 de septiembre, que volcó repentinamente a 16 millas de Cabo Prior arrojando al mar a sus siete tripulantes, con el resultado de seis rescatados y un fallecido. La comisión también investiga los sucesos de los siguientes pesqueros gallegos: el José Almuíña, el Rosamar, el Monte Galiñeiro, el Canconio, el Villa de Aguete, el Furacán y el Nosa Cantiga.

Las investigaciones de accidentes marítimos que ayer publicó el Ministerio de Fomento pertenecen a 39 siniestros producidos entre 2000 y 2008 en las costas españolas o en aguas internacionales pero en los que se vieron involucradas embarcaciones de pabellón español. 

Los informes recogen los resultados de pequeños incidentes de motos acuáticas en aguas españolas, las causas de otros con importantes repercusiones medioambientales como el Prestige y otros muchos naufragios de pesqueros españoles en los que se registraron muertes de algunos de sus tripulantes. 

Entre los accidentes de buques de pesca españoles más conocidos y con más muertes están el del Nuevo Pilín, que se produjo en noviembre de 2004, y el del Nuevo Pepita Aurora, el cinco de septiembre de 2007. 

El Nuevo Pilín se hundió con cinco tripulantes a bordo en aguas del Cantábrico y como consecuencia del accidente tres marineros murieron y los otros dos fueron dados por desaparecidos. La causa del naufragio fue la pérdida de estabilidad del buque después de que entrase gran cantidad de agua en la embarcación y que esta no cumpliese con los criterios de estabilidad establecidos para este tipo de buques. 

El Nuevo Pepita Aurora volcó cuando regresaba a Barbate tras faenar en los caladeros marroquíes y arrojó al mar a sus 16 tripulantes. El barco quedó quilla al sol durante un día hasta que se hundió mientras que cinco tripulantes fallecieron y otros tres desaparecieron. El buque tenía una mala distribución de los pesos a bordo y el fuerte oleaje provocó su escora y posterior vuelco.

Desarrollo histórico de la estabilidad del buque

Desde hace muchos años el hombre se ha preocupado por buscar explicaciones a las cosas cotidianas que nos rodean, tanto para saber el porqué de las cosas como para buscar una evolución y mejora de dichos elementos. Cogiendo como referencia la tesis de Claudio Alexis Rodríguez Castillo titulada “Análisis de la estabilidad de pesqueros en olas regulares de proa” [8] para llevar a cabo un resumen histórico de la evolución que ha habido en el estudio de éste tema se ve una lenta progresión hasta  el siglo XX. Desde entonces, la necesidad de hacer la navegación más segura acorde con la evolución de las nuevas tecnologías ha dado pie a que se creen grupos dedicados al estudio y mejora de este apartado de la navegación náutica publicando normas y criterios aplicados internacionalmente. Se podría decir que todo comenzó por Arquímedes (287-212 AC), que en su tratado “Sobre los Cuerpos Flotantes” fue uno de los primeros en dejar constancia del estudio y análisis de la estabilidad de los buques, donde estableció una explicación científica y el cálculo cuantitativo de la estabilidad hidrostática. [9] en el ámbito de todo el mundo. [21]

Como resultado de la buena labor ejercida en estas conferencias, las actas de las STAB y de los ISSW representan una fuente fundamental y única de la información y el conocimiento para todos aquellos que están involucrados, obtiene la intención de participar, en la investigación básica y aplicada, la evolución de la regulación, u otras actividades consideradas de contribución al cuerpo de conocimiento y comprensión del tema de la estabilidad y la seguridad de los buques. [21]
Aunque los resultados logrados por estos trabajos son relevantes y del punto de vista

práctico la introducción de los estándares internacionales de la IMO haya significado un incremento en la seguridad de los buques, continúan ocurriendo accidentes relacionados con la estabilidad del buque, inclusive en casos donde se ha cumplido con los criterios de estabilidad y normas de seguridad. Por eso, nuevos retos van surgiendo a medida que nuevas formas y tipos de buques aparecen.

PRINCIPIOS DE ESTABILIDAD DEL BUQUE COMO CUERPO FLOTANTE 1

Principales Centros del Buque

     

ESTABILIDAD

Es la tendencia que debe tener el buque en recobrar su posición inicial cuando ha sido
apartado de ella por acción de fuerzas exteriores como puedan ser la mar o el viento.
CLASIFICACIÓN DE LA ESTABILIDAD (F.P.)
Atendiendo al concepto de estabilidad podemos distinguir:
a) Estabilidad estática, el conjunto de fuerzas que actúan sobre el barco en una escora
determinada.
b) Estabilidad dinámica, el trabajo que hay que efectuar para llevarlo desde el ángulo de
inclinación hasta la posición de equilibrio.
A su vez, la estabilidad estática puede clasificarse en:
Inicial (escoras < 10°)
Estabilidad transversal
Grandes escoras > 10°
Estabilidad
Estabilidad longitudinal
LOS CUATRO PUNTOS FUNDAMENTALES EN LA ESTABILIDAD DE UN BUQUE
Estos puntos son todos imaginarios, o sea no
pueden ser vistos ni están marcados en ninguna
parte del buque.
Punto K
Es el punto de partida para la medición de los tres
puntos restantes que interesan a la estabilidad del
buque. Se encuentra sobre la línea de intersección
del plano de crujía y el plano base.
Las ordenadas de dichos tres puntos son medidas
desde allí, a partir de ahora lo denominaremos «K» (keel).

PUNTO B Ó C

Está en el centro geométrico de la obra viva o carena. Se lo denomina «Centre of

bouyancy», baricentro (B) ó centro de carena (C). No confundir con centro de flotación

(Centre of flotation).

Sobre el actúa la resultante de todos los empujes hidrostáticos verticales, de abajo hacia

arriba que actúan en la carena.

Como ya se vio, la masa de agua desplazada por la carena es igual a la masa del buque.

Esto significa que el agua desplazada por la carena pesará exactamente lo mismo que el

buque.

Cabe destacar que el baricentro se mueve en todos los sentidos cuando el buque navega en

aguas agitadas, cuando el buque se escora y/ o cabecea debido a fuerzas externas.

La distancia del mismo hasta K es la ordenada del baricentro (KB) ó (KC) y su dimensión en

buques mercantes convencionales es aproximadamente 0,53 del valor del calado medio

(debido a la curvatura del los pantoques).

Si la carena fuera un prisma rectangular, su valor sería exactamente del calado medio.

Su valor se obtiene de las Curvas de Atributos de Carena Derecha o de tablas

 

PUNTO G

Es el centro de gravedad (CG)(Centre of gravity). Desde el actúa la resultante de la fuerza de

gravedad sobre todas las diferentes masas que componen el buque.

Su posición respecto a la quilla es conocida como la ordenada del centrode gravedad (KG) y

es registrada en los libros de estabilidad del buque para desplazamiento liviano, debiendo el

oficial calcularla de acuerdo a como haya procedido a cargar su buque.

PUNTO M

Cuando el baricentro se mueve ligeramente debido a pequeñas escoras o cabeceas (5°a

10°), la vertical que partiendo del baricentro cruz a el plano de crujía lo hace en un punto que

se mueve muy poco.

Este punto es conocido como «Metacentro», M, (Metacentre).

Lo podemos definir como la meta superior que puede alcanzar el centro de gravedad CG

para que el buque genere brazos adrizantes, si lo sobrepasa cuando el buque escore

generará brazos escorantes.

2Apuntes de Estabilidad

La distancia de la quilla al meta centro es la ordenada meta céntrica (KM), y está registrada

en los libros de estabilidad del buque para diferentes condiciones de carga.

La distancia entre CG y M se denomina altura metacéntrica, GM, y nos permite controlar

convenientemente la seguridad y el confort del buque.

Todo buque, dentro de sus protocolos, indica los valores máximo y mínimo aconsejables

para el mismo.

Si el buque escora o cabecea ángulos mayores a los mencionados, entonces el metacentro

comienza a «deambular» dejando ya de ser un punto prácticamente fijo.

CENTRO DE GRAVEDAD

Analicemos ahora con mayor profundidad el centro de gravedad, ya que este es el punto sobre el cual el marino debe trabajar.

De acuerdo a como arrume la carga y maneje los pesos a bordo, moverá, tanto vertical como transversal mente, dicho punto.

Todo objeto tiene un centro de gravedad.

Para objetos sólidos, uniformes, como una esfera o una caja, el centro de gravedad estará en el centro geométrico de ese objeto.

Para objetos más complejos, el centro de gravedad puede ser determinado sumando todos los pesos juntos, encontrando un punto promedio, donde actuará la fuerza de gravedad.

Para los buques, se hace a través de complejos métodos y lo hace el ingeniero naval calculándolo para el buque cuando sale del astillero, desplazamiento liviano (Light ship).

Cuando el buque flota en reposo en el agua, un empuje vertical de abajo hacia arriba actúa e iguala a la fuerza de gravedad que actúa verticalmente de arriba hacia abajo.

Entonces el buque flota.

Obviamente en un buque durante un viaje hay muchos pesos que son agregados y removidos.

Se consumirá combustible desde los dobles fondos, lo que hace que el centro de gravedad suba; el buque se hace más liviano y por eso el buque disminuye su calado y el baricentro (B), en consecuencia, baja. En un pesquero, por ejemplo, además de consumir combustible, cargará toneladas de pescado lo que, según la ubicación del mismo, podrá producir un efecto contrario.

A causa de esos factores, los centros de gravedad y baricentro, pueden ser desplazados considerablemente con respecto a los valores registrados del buque en el momento de la zarpe, y el oficial deberá estar atento a dichos cambios.

MOMENTOS

«Momento» es el producto de un peso o una fuerza, por la distancia desde donde actúa, con respecto a un punto.

Por ello es imprescindible entender el concepto de los momentos cuando tratamos la estabilidad del buque.

Consideremos una barra de peso despreciable de 2 m. de longitud, apoyada en un fulero y equilibrada.

Si le colocamos una masa de 1 Kg. a una distancia de 0,8 m. del apoyo, entonces la barra estaría desequilibrada.

Es obvio que necesitaríamos otra pesa de 1 Kg. del otro lado de la barra y a igual distancia(0,8 m.) del fulero para equilibrarla. Matemáticamente decimos que está en equilibrio cuando la suma de los momentos anti-horarios (Anti-eloekwise I eounter-eloekwise) es igual a la suma de los momentos horarios (Cloekwise).

Entonces tomando los momentos respecto del fulero, el momento antihorario es exactamente el mismo que el momento horario. La barra estará balanceada.
 Ver también al colega Harry Gonzalez en: http://estabilidadbuque.blogspot.com/ 
 

 

ESTABILIDAD INICIAL

La estabilidad transversal se ha dividido en inicial y para grandes escoras, según sea el ángulo de escora inferior o superior a 10-15, y ello es debido a que durante los 10-15 primeros de escora las verticales trazadas desde las sucesivas posiciones del centro de carena se cortan aproximadamente en un mismo punto llamado Metacentro, pero al ser mayores los ángulos de escora, el corte entre las verticales de las distintas posiciones de C, se hace en puntos diferentes.

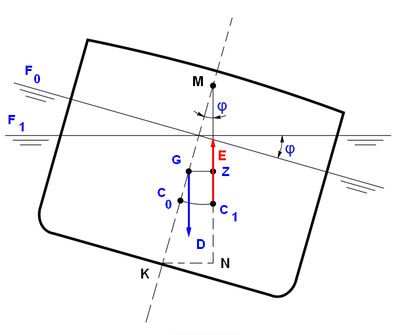
PAR DE ESTABILIDAD

Si un buque adrizado escora un ángulo I inferior a 15°, pasará de la flotación LF a L'F' y el desplazamiento continuará actuando en G por no

haberse variado la posición de los pesos.

Por el contrario, el centro de carena (C) variará su posición pasando a C'. En este momento, la nueva vertical del empuje del agua corta al plano diametral en un punto llamado metacentro (M).

Observando la figura veremos que el Desplazamiento (D) está actuando hacia abajo sobre G, y el empuje (E) sobre C' y hacia arriba, creando de este modo un par de fuerzas, cuyo brazo es el GZ. Este brazo será perpendicular a la vertical del empuje (E), y al actuar sobre el buque lo hace girar en el sentido de la flecha, adrizándolo. Momento del Par de Estabilidad Me = D x GZ.

    

BRAZO ADRIZANTE

Habiendo estudiado los conceptos básicos de centro de gravedad, baricentro, meta centro y punto K, podemos estudiar como se genera el «brazo adrizante».

Cuando el buque flota en aguas tranquilas y adrizadas, se encuentra en equilibrio y quieto.

La masa del buque es igual a la masa del agua que desplaza y en consecuencia la fuerza de gravedad y el empuje hidrostático son iguales y de sentido inverso actuando sobre una misma vertical.

Estará adrizado si su centro de gravedad y su baricentro se encuentran sobre el plano de crujía.

Si en cambio el centro de gravedad está desplazado hacia una banda el buque estará en reposo pero con una escora permanente hacia la banda donde el mismo esté desplazado(Iist), actuando tanto el empuje hidrostático como la fuerza de gravedad sobre la misma vertical Pero si al buque lo escora una fuerza externa (heel), el baricentro se moverá hacia la banda sumergida, aunque el centro de gravedad permanezca estático (siempre que nada se mueva sobre el barco como superficies libres, pesos suspendidos o carga que se desplace) se crea una fuerza que intenta llevar al buque a su posición de equilibrio.

La distancia horizontal entre las dos fuerzas verticales, una hacia arriba (empuje hidrostático) y la otra hacia abajo (fuerza de gravedad), es conocida como «brazo adrizante» GZ.

Cuanto mayor sea el brazo adrizante, más rápidamente buscará el buque la posición de adrizamiento, haciendo su período de rolido menor.

METACENTRO (M)

Como definición, entenderemos que el metacentro es el punto donde confluyen el plano diametral del buque y la vertical trazada desde el centro de carena, cuando éste último ha sido desplazado a causa de una escora, siendo M el punto máximo hasta donde puede llegar el centro de gravedad (G) para que el buque sea estable.

La distancia CM o radio metacéntrico, así como KC, se encuentran en las curvas hidrostáticas mientras que la distancia KG es la altura del centro de gravedad sobre la quilla, por lo que la altura metacéntrica (GM) será la diferencia entre KM y KG.

KM = CM + KC

GM = KM - KG

ALTURA METACÉNTRICA

Altura metacéntrica transversal inicial: Se define así al segmento

. Es la ubicación relativa de dos puntos importantísimos para definir el equilibrio de un cuerpo flotante. El primer punto es el centro de gravedad (G) y el otro el metacentro transversal inicial con ordenadas KG y KM respectivamente.

Si tomamos como origen de las coordenadas a la línea base tendremos que:

Al efecto de analizar el equilibrio de un buque

podemos afirmar que el mismo será:

• Estable si

• Inestable si

• Indiferente si

Según sea la altura metacéntrica, positiva, negativa o nula

CASOS DE EQUILIBRIO: ESTABLE, INESTABLE E INDIFERENTE

La condición de estabilidad de un buque depende del par de estabilidad y éste depende de las posiciones del centro de gravedad y centro de carena. Para los diferentes casos podemos distinguir los equilibrios siguientes:

K

1.- EQUILIBRIO ESTABLE O 2.-EQUILIBRIO INDIFERENTE 3.- EQUILIBRIO INESTABLE

ESTABILIDAD POSITIVA O ESTABILIDAD NULA O ESTABILIDAD NEGATIVA.

Cuando al escorar un buque, a En el caso de que coincidan G y Cuando el centro de gravedad causa de una fuerza exterior, M no se genera ningún par de se halle más alto que el M se encuentra situado por fuerzas por lo que el buque metacentro, el par de encima de G, el brazo del par quedará en la posición escorada. estabilidad hará girar el barco generado hace adrizar al GM nulo en el sentido de la flecha y por buque.

tanto aumentaría su escora.

GM + KM=KG

KM > KG

GM - KM < KG.

MOVIMIENTO DE PESOS A BORDO Y SU INFLUENCIA EN LA ESTABILIDAD, ESCORA

Y EL ASIENTO

Para poder comprender el movimiento de pesos a bordo, es mejor estudiarlos según sus tres

coordenadas, vertical (K), longitudinal (ƒ) y transversal (¢).

Este movimiento de pesos que puede ser debido a dos causas:

Carga y/o descarga.

Traslado.

Afecta a la estabilidad, escora y asiento del buque.

                       

TRASLADO DE PESOS

En el traslado de pesos dentro de un barco tanto sea en sentido vertical, longitudinal o transversal, se cumple que, no hay variación del Desplazamiento, pero si hay variación en la posición del Centro de Gravedad.

El movimiento del Centro de Gravedad está en función de:

P = Peso en Tm.

d = distancia del peso en mts.

D = desplazamiento en Tm.

 

TRASLADO VERTICAL

El traslado vertical de un peso en un barco hará subir o bajar el Centro de Gravedad.

Afecta a la Altura Metacéntrica (GM), teniendo en cuenta que, si bajamos el Centro de Gravedad (G), tendremos mayor altura

metacéntrica (GM) y mayor brazo del par de estabilidad (GZ) por lo que al escorar, habrá mayor par adrizante, y por lo tanto tendrá mayor estabilidad.

Si subimos pesos asciende el G, disminuye GM y GZ, por lo que, al escorar habrá menor par adrizante y menor estabilidad.

Navegando podemos determinar que si los períodos de balance duran de 4 a 5 seg., éstos son muy perjudiciales por ser muy violentos, pudiendo producir corrimientos de carga, vibraciones, accidentes, etc. A estos buques se les llama buques duros, incómodos pero muy estables.

A medida que aumenta el período de balance, hay menos peligro de movimiento de carga, es más cómoda la navegación pero la estabilidad disminuye dando lugar a los buques blandos, confortables pero inestables.

TRASLADO TRANSVERSAL

El traslado transversal de un peso en un barco provocará una escora del mismo hacia la banda que ha sido desplazado el peso, también a la estabilidad cuando el barco balancea hacia la banda escorada (disminuyendo GZ).

El cálculo del ángulo de la escora (I) se hará de forma práctica, con un clinómetro, o siempre y cuando sea inicial, podremos averiguarlo en base al triángulo GG'M:

La translación de un peso ya existente a bordo siempre puede descomponerse en tres ejes principales: Transversal, Longitudinal y Vertical. Analicemos en esta oportunidad la traslación transversal. Las translaciones de pesos en un buque pueden tener efecto sobre uno o más de los parámetros detallados.

La altura metacéntrica.

La escora.

El asiento.

Translación transversal: Supongamos un buque con

desplazamiento (D) en equilibrio y adrizado, en el que se traslada un peso (W) ya incluido en (D) en el sentido de babor a estribor o viceversa una distancia (d) a la posición (w') (fig 1). El centro de gravedad (G) del conjunto sufrirá también un desplazamiento (GG').

Teorema de la translación: Si en un conjunto de pesos se mueve uno de ellos (W), el centro de gravedad del conjunto (G) se moverá paralelamente y en el mismo sentido una distancia (GG') igual a la del peso parcial multiplicada por la relación entre dicho peso parcial y el peso total del conjunto.

A consecuencia de esta translación el buque experimentará una escora a la banda en que fue movido el peso, de manera tal que la vertical del centro de gravedad desplazado (G') y en centro de empuje (B') vuelvan a alinearse (fig 2) recuperándose una nueva condición de equilibrio.

Para pequeños ángulos de escora podrá decirse entonces que:

por tanto:

Donde:

es la altura metacéntrica inicial.

Esta fórmula permite obtener la escora producida por el desplazamiento transversal de pesos.

A = C pp - C pr

a = A f - A i

A = Asiento en cm.

a = alteración en cm.

TRASLADO LONGITUDINAL

El traslado longitudinal de un peso en un barco, origina una alteración en el asiento y por lo tanto un cambio en los calados.

El asiento será de signo positivo o apopante si el calado de popa es mayor que el de proa.

Por el contrario, será de signo negativo o aproante si el calado mayor es el de proa.

Cuando se deban trasladar pesos a bordo se calculará el asiento previamente.

Cada buque tendrá calculado su Momento Unitario (Mu), que definimos como el producto del peso, en toneladas, por la distancia de traslado, en metros, necesarios para variar el asiento del buque 1 cm. De ahí que para calcular la alteración(a) al  efectuar un traslado de pesos lo podemos calcular con la siguiente fórmula:

P = peso trasladado enTm

a = alteración en cm

dl = distancia en m

Mu = Momento unitario en Tm x m

CARGA O DESCARGA DE PESOS

Al cargar un peso aumentamos el D y para efectos de cálculo, será lo mismo que cargarlo en el centro de gravedad produciendo una inmersión y después trasladarlo al punto correspondiente.

Al descargar un peso, será lo mismo que trasladarlo al centro de gravedad y desde ahí descargarlo, produciendo una emersión.

Para calcular la inmersión o la emersión producida en la carga o descarga de pesos lo haremos a través de las siguientes fórmulas:

TONELADAS POR CENTÍMETRO (TC)

Son el número de toneladas a cargar o descargar para que el calado medio varíe un centímetro.

CENTRO DE FLOTACIÓN (CF)

Es el centro de gravedad de la superficie de flotación, es decir el punto sobre el cual el buque pivotará al cabecear. Si cargamos un peso sobre este punto el buque no variará el Asiento.

ESTABILIDAD ESTÁTICA TRANSVERSAL INICIAL

Esta estabilidad se considera cuando el buque sufre escora s inferiores a 10 o el metacentro

M no cambia de posición, el brazo de adrizamiento GZ en el triángulo rectángulo GZ M de la

Fig. 2 se halla mediante la relación trigonométrica: GZ = GM sen θ

El momento adrizante viene dado por el par de estabilidad que se crea al escorarse el

buque:

M a = D x GZ = D x GM sen θ M a = momento adrizante

D = desplazamiento

GM = altura metacéntrica

θ = ángulo de escora inferior a 10o.

Fig. 2

EJEMPLO N° 1 Un buque de 1.000 Tm. de desplazamient o tiene un GM = 1m.

Hallar su momento adrizante y brazo de adrizamiento para 6 grados de escora.

M a = GM x sen θ x D = 1 x sen 6° x 1.000 = 1 x 0,1045 x 1.000 =

M a = 104,5 tonelametros

GZ = GM x sen θ = 1 x sen 6° = 1x 0,1045 = 0,1045 m.

EFECTO DE SUPERFICIE LIBRE SOBRE LA ESTABILIDAD

Cuando un tanque abordo se encuentra parcialmente lleno, y la superficie del líquido contenido en su interior esta libre de mantener la horizontal durante el movimiento de rolido, se experimenta una pérdida de estabilidad o disminución del brazo (GZ') de la cupla adrizante.

Para estudiar este efecto supóngase una buque cuyo corte trasversal es el de la figura 1. El mismo posee una altura metacéntrica inicial (GM).Un tanque parcialmente lleno cuya superficie (ab) se encuentra horizontal.

Si el buque es apartado de su vertical, un ángulo pequeño (θ), la superficie del líquido adoptará una nueva posición (a"b") manteniendo la horizontalidad y verificándose que la cuña de basetriangular (a"a'o) y de eslora (longitud) igual a la del tanque se desplaza a una nueva situación (b"b'o).

El centro de gravedad (g) de la cuña (a"a'o) se desplaza a (g'), por lo que a los fines del análisis es como si se tratara de una traslación trasversal de pesos, por esta razón el centro de gravedad del buque también experimenta un corrimiento hacia la banda de escora

representado en la figura 2 por el segmento (GG').

Nótese que este desplazamiento lateral puede visualizarse como si fuese una elevación del centro de gravedad del buque a una nueva posición (Gv), el brazo de la cupla adrizante es ahora (G'Z') o (GvZ).

Entonces se ve claramente que acción o efecto de una superficie libre genera la elevación virtual del centro de gravedad con la consiguiente pérdida de estabilidad.

Puede demostrarse que el segmento (GGv) que representa la elevación virtual del centro de gravedad debido al efecto de la superficie libre esta dado por:

Donde:

• γ t : Es el peso específico del líquido contenido en el tanque.

• γ f : Es el peso específico del agua en la que flota el buque.

•

i: Es el momento de inercia de la superficie libre del líquido con respecto a su eje baricéntrico paralelo a la crujía.

•

V: Es el volumen de la carena del buque.

Dado que: γ f * V = ∆ o sea el desplazamiento del buque, entonces:

Esta fórmula representa el valor de la pérdida de GM producida por la superficie libre en un tanque, si la misma situación se repite en varios de los tanques de un buque en forma simultánea, esto es, que varios tanques están parcialmente cargados entonces la perdida total estará expresada por:

El efecto de superficie libre se verifica en cualquier tanque lleno con más de un 5% y hasta un 95% de su capacidad. Es obvio que si el tanque se encontrara a máxima capacidad el líquido en su interior se comportaría como un sólido y el efecto de superficie libre desaparece.

Nótese que el momento de inercia de una superficie esta dado entre otros parámetros por el cubo de la manga del tanque, es decir la manga elevada a la 3 por este motivo el efecto de superficie libre es mayor cuanto más ancho es el tanque. (Ver momentos de inercia de

superficies).

Debido al efecto de superficie libre y con el fin de disminuir la pérdida de estabilidad, se recomienda:

• Limitar la cantidad de tanque en servicio con cargamento parcial.

• Subdividir en el sentido de la manga los tanques de carga.

• Completar con lastre los doble fondos

PESO DEL LIQUIDO QUE ES NECESARIO CARGAR O DESCARGAR EN UN TANQUE DETERMINADO PARA COMPENSAR LA PERDIDA DE ESTABILIDAD POR SUPERFICIE LIBRES.

Supuesto el tanque vacío, se calcula inicialmente el efecto por superficies libres sin tener en cuenta el cambio del desplazamiento, por la adicción del peso representado por el líquido embarcado en el tanque.

↑ G 0 G 1 = i δ /∆ 0

Tenemos que hacer bajar el centro de gravedad el valor ↓ G 1 G 0 mediante el peso del liquido, suponiendo constante la subida por superficies libres.

↓ G 1 G 0 = p x d v / (∆ 0 + p)

(G 1 G 0 ) (∆ 0 + p) = p x d v

∆ 0 x G 1 G 0 + p x G 1 G 0 0 p x d v

∆ 0 x G 1 G 0 = p(d v – G 1 G 0 )

p = ∆ 0 x G 1 G 0 / d v – G 1 G 0

Errores cometidos en la fórmula:

a) No haber tenido en cuenta el cambio de dv por haber aumentado el nivel del líquido en el tanque.

b) No haber tenido en cuenta la variación de ↑ G 0 G 1 = i δ / ∆ 0 + p 

Con el peso calculado por la formula aproximada, hallamos el valor de la bajada mas

exactamente.

↓ G 1 G 0 = p d v / ∆ 0 + p

Cálculo del Kg del líquido del tanque:

p = v x δ; v = p/δ; h = v / e x m; Kg = 1/2 h

Como conocemos el valor KG 0 , d v = KG 0 –

Kg

La subida de ↑ G 0 G 1 = i δ / ∆ 0 + p ; si comparamos esta subida con la bajada anterior, y la diferencia está dentro de los milímetros, nos basta, sino verificamos una nueva aproximación. Normalmente basta con una primera aproximación, teniendo en cuenta también que la aproximación en milímetros sobre la estabilidad, que dan las oficinas técnicas, no deja de ser demasiado optimista.

SUPERFICIES LIBRES

Todos los buques en servicio tienen tanques y doble fondos que contienen líquidos que

pueden ser combustibles, agua dulce, agua de lastre, aceites y otros.

Fig. 3

Estos líquidos al encontrarse en los tanques se comportan como sólidos cuando los

mismos se hallan llenos pero cuando los tanques tienen líquidos que no completan su

capacidad al moverse el buque en sus balances o cabeceos los líquidos contenidos en

los tanques tratan de conservar la superficie horizontal. A los tanques que se

encuentran a media capacidad o que no están llenos se dice que tienen superficies

libres. Estas superficies libres son enemigas de la estabilidad porque siempre que ellasexistan en los buques va a haber pérdida de la estabilidad.

Supongamos en la Fig 3 el tanque que tiene un líquido de peso p. no se encuentra lleno

al escorarse el buque un ángulo " la superficie del tanque ab que tenía cuando el buque

se hallaba adrizado va a cambiar a cd, manteniéndose paralela a la línea de flotación L

'F'.

El centro de gravedad del buque G se trasladará a G", porque la cuña de agua que

estaba en aoc se trasladó a bod y el centro de gravedad g del líquido del tanque con

superficie libre, se corrió a g' creciendo el momento escorante:

p x gr = p x gm x sen θ

Al producirse este par escorante por haberse trasladado el centro de gravedad del líquido de gag', debido al teorema de traslado de un peso dentro de un sistema de

pesos el G del buque se trasladará a G" como se dijo anteriormente en una dirección

paralela a los centros de gravedad de las cuñas de agua y en el mismo sentido y por la

misma razón paralelo a gg'.

El peso del buque D 1 estará aplicado en G" y el nuevo momento de estabilidad será:

Me' = D x G"Z. la distancia G"Z = G'Z' por ser paralelas entre paralelas, entonces Me'

= DxG'Z'.

El momento de estabilidad del buque Me sin superficie libre es igual a:

Me = D x GZ

Estableciendo la igualdad de momentos, tenemos:

Me' = Me - momento escorante

D x G'Z' = DxGZ – p x gr

D x G'M x senθ = D x GM x senθ – p x gm x senθ

Dividiendo los dos miembros de esta igualdad por D x senθ nos queda:

G'M = GM – p x gm = GM - GG'

D

Me' = Momento de estabilidad al escorarse un ángulo 0o con superficie libre

Me = Momento de estabilidad al escorarse un ángulo θ , sin superficie libre

θ = Angulo de escora pequeño que no sobrepase la estabilidad inicial

p = Peso del líquido del tanque

gm = Radio metacéntrico del volumen del líquido del tanque.

Como podemos apreciar, la altura metacéntrica inicial GM ha disminuido debido a un

ascenso del centro de gravedad del buque de G a G', esta elevación se dice que es virtual

debido a que se considera como que si se elevara el centro de gravedad g del líquido del

tanque hasta m, el cual representa el metacentro del volumen del líquido del tanque.

Cálculo de la subida virtual GG' por efecto de las superficies libres de los líquidos

Vimos anteriormente que la subida virtual de G era: GG' = p x gm

D

gm = i por ser el radio metacéntrico del volumen del líquido del tanque

v

i = momento de inercia de la superficie libre del líquido del tanque.

v = volumen del líquido del tanque

δ = densidad del líquido del tanque

Sustituyendo el valor de gm = i / v y p = v x δ, se tiene:

v x δ x i

GG’ = p x gm =

D

v

D

= δ x i

D

La altura del centro de gravedad del buque KG c corregida por superficies libres se obtiene:

δ x i

Para un tanque: KG c = KG + D ; si fueran varios tanques:

1

D = ∆

KG c = KG + Σ δ x i

D Como podemos observar la pérdida de estabilidad de un buque ocasionada por superficie

libres de los líquidos en los tanques

GG’ = Σδ x i, es directamente proporcional a la densidad δ y al momento de D inercia i, e inversamente proporcional al desplazamiento D, siendo independiente del

volumen del volumen que posea el tanque.

CURVAS CRUZADAS DE ESTABILIDAD O CURVAS KN

Las curvas cruzadas de estabilidad se calculan cuando se construye el buque y se presentan

en un par de ejes coordenados cartesianos. (Fig. 4).

Fig. 4

En las abscisas representan las toneladas de desplazamiento (D) y en las ordenadas los valores de los brazos KN en metros o pies.

Cada curva viene dada para un determinado ángulo de escora, en el ejemplo de referencia están las curvas cada 15 grados de escora, en ciertos buques se calculan cada 10 grados.

Fig. 5. 

Criterios de Estabilidad: es el conjunto de normas que debe cumplir un buque para que su estabilidad alcance valores mínimos que garanticen su seguridad.
Estos criterios pueden clasificarse según los parámetros que controlan en:

• Criterios en función de la altura metacéntrica.
• Criterios en función de la estabilidad estática.
• Criterios en función de la estabilidad estática y dinámica.
• Criterios en función de la estabilidad estática y la acción del viento.
• Criterios en función del período y amplitud del balance.

Existen también diferentes criterios creados para distintos tipos y tamaños de embarcaciones, dado que es muy amplia la variedad de buques y muy difícil que un solo criterio puede ser aplicado de forma universal.
Así distinguimos:

Índice

• 1 Criterio de Rahola
• 2 Criterio de la OMI
• 3 Criterio de Nickum para buques pesqueros
• 4 Criterio holandés (para buques costeros de menos de 500 T.R.B.)
• 5 Bibliografía consultada

Criterio de Rahola[editar]

Curvas de estabilidad y míminos de Rahola.

Es el criterio ideado por el profesor finlandés Rahola quien analizando la pérdida de numerosas embarcaciones por falta de estabilidad y sugirió un criterio basado en los brazos adrizantes (corregido por superficies libres), y el ángulo de inundación.

• Valores mínimos de GZ para los ángulos de escora:

Escora = 20(grados)	GZ = 14 cm
Escora = 30(grados)	GZ = 20 cm
Escora = 40(grados)	GZ = 20 cm

• El máximo de la curva de brazos GZ deberá estar comprendido entre los ángulos 30º y 40º
• El brazo dinámico para 40º debe ser como mínimo 8 cm/radián. Si el ángulo de inundación es menor a 40º.

En la figura de la derecha se muestran tres curvas correspondientes a tres buques, A y C cumplen parcialmente con los criterios de Rahola mientras que solo B satisface todos los requisitos.

Criterio de la OMI[editar]

La Organización Marítima Internacional, (OMI) fijó un criterio de orden mundial para los buque de pesca, carga y pasajeros menores a 100 m de eslora.
Este criterio puede ser resumido en las siguientes pautas:

• La altura metacéntrica corregida por superficies libres debe ser mayor a 0,35 m
• El máximo valor de la curva de brazos GZ será para las escoras de 30º o más
• La curva de brazos GZ a partir de 30º deberá tener brazos mayores de 0,20 m
• El área encerrada por la curva de brazos GZ y la ordenada de 40º será igual o mayor a de 0,090 m*radián.
• El área encerrada por la curva GZ y las ordenadas de 30º y 40º de escora y/o la ordenada correspondiente al ángulo de inundación (si fuera menor a 40º) deberá ser mayor de 0.030 m*radián.
• El área encerrada por la curva de brazos GZ y la ordenada de la escora de 30º será igual o mayor a 0,055 m*radián.

La OMI fija además las forma en que debe corregirse la altura metacéntrica por la acción de superficies libres.

Criterio de Nickum para buques pesqueros[editar]

Este criterio establece que un buque pesquero en servicio debe cumplir con:

• Primero:

durante la condición más crítica de trabajo:

• • a) La altura metacéntrica GM debe ser igual o mayor que 0,1 de la manga o igual o mayor de 0,610 m
  • b) Debe cumplirse la relación: ${\displaystyle {\frac {F}{M}}+{\frac {A}{E*M}}\geq 0,15}$

Donde:

• • • GM = Altura metacéntrica inicial.
    • M = Manga de trazado.
    • F = Francobordo.
    • A = Área de la obra muerta proyectada sobre el plano diametral.
    • E = Eslora entre perpendiculares.

• Segundo:

lo estipulado en el punto primero debe complementarse con las mediciones de GM efectuadas para la condición de carga más crítica. Para la determinación del GM se aplicara la siguiente fórmula: ${\displaystyle GM=\left({\frac {K*M}{T}}\right)^{2}}$ Donde:

• • • K = 0,40 si M está expresado en pies y 0,80 si M está expresado en metros
    • M = Manga de trazado (expresado en pies o metros)
    • T = Período de oscilación completa expresado en segundos (promedio observado de 20 oscilaciones).
    • GM = Altura metacéntrica que quedará expresada en la misma unidad que lo fue la manga

Criterio holandés (para buques costeros de menos de 500 T.R.B.)[editar]

Este es el criterio ideado por la autoradad holandesa que es aplicable a buques con un tonelaje inferior a 500 T.R.B. (Tonelaje de Registro Bruto). La curva de brazos adrizantes, en las peores condiciones, debe cortar o ser tangente a la línea definida por los siguientes puntos,

Escora = 0 (grados)	GM = 0,44 m
Escora = 35 (grados)	GZ = 0,22 m
Escora = 60 (grados)	GZ = 0,27 m

Este es un criterio muy similar al de Rahola, de fácil interpretación.

 

EJERCICIOS

1. El atunera «Aratz» tiene un desplazamiento de 2.280 Tm. y un KG = 5,05 m. Calcular la altura metacéntrica. Ver fig. Nr.5.

R.: GM = 0,47 m.

2. Hallar el brazo de adrizamiento (GZ) del ejercicio anterior cuando el buque se escora 8 grados.

R.: GZ 8o = 0,065 m.

3. Hallar el brazo GZ para 20 grados de escora del atunera «Aratz» sabiendo que tiene un desplazamiento de 2300 Tm. y un KG = 5,00 m.

R.: GZ 20o = 0,19 m.

4. El buque de la Fig. 5 tiene un desplazamiento de 8000 L/T y un KG = 22' 06". Calcular el brazo de adrizamiento a los 15 grados de escora.

R.: GZ 15o = 0,76 pies = 9,1".

5. Una gabarra de 3500 Ton. de desplazamiento tiene tres (3) tanques con gasolina de

densidad δ = 0,780 con superficie libre 5 m. de eslora por 4 m. de manga cada uno y dos tanques con fuel oil de densidad o,97 con superficie libre de 4 m. de eslora por 3 m. de manga cada uno. Su KG = 3,00 m. y KM = 5,00 m.

Hallar: GMc y Variación del brazo GZ al dar un bandazo de 20o.

R.: a) GMC = 1,977 M.; B) Disminuye el brazo GZ a 20o = 0,008 m.

6. Un buque de 1000 ton. de desplazamiento tiene un GM = 1 m. Hallar su momento adrizante y brazo de adrizamiento para 6o de escora.

7. El buque ENN, en cierto estado de carga, tiene un desplazamiento de 6.200 ton. en agua salada (δ= 1,025 Ton/m 3 ) y su KG es de 5,40 m., pero se encuentra desplazado 0,60 m.

a babor de su línea de crujía.

Determinar el ángulo θ de escora permanente que adopta.

R.: θ= 15o

8. Cierto buque se halla con un calado medio de 4,00 m., correspondiéndole un

desplazamiento de 5.350 ton.

Se lastra el doble fondo No 8 con 100 ton., siendo el Kg del mismo de 0,60 m.

Si el KG i del buque era de 5,80m. ¿Cuál será el KG f ?

R.: KG f = 5,70 m.

9. Calcular la posición definitiva del KG f de un buque cuyo calado medio es de 5 m. correspondiéndole un desplazamiento de 6900 ton.

Su KG es de 6 m.

Se descargan 500 ton., de la bodega No 1 cuyo Kg es de 4,30 m.

R.: KG f = 6,13 m.

10. En la prueba de estabilidad del buque ENN el mismo tenia un calado medio de 3,20 m. y su KG por cálculo es de 4,35 m.

Se desea conocer el peso que deberá transportarse transversalmente desde crujía para que, desplazándose 8,00 m., le produzca una escora de 2o.

R.: w= 84,5 ton.

11. Un buque de 8153,75 ton. de desplazamiento tiene un KM = 8,00 m. y un KG = 7,50 m.

En el hay un doble fondo de 15 m. de eslora, 10 m. de ancho y 2 m. de alto que está lleno con agua de mar (1,025 ton./m3)

Hallar el nuevo GM si se deslastra 1 m.

R.: GM v = 0,22 m.

12. Un buque de 8.000 ton. de desplazamiento tiene un KM de 7,5 m . y un KG de 7,0 m.

Un tanque doble fondo de 12 m. de eslora, 15 m. de manga y 1 m. de puntal, dividido en su sección media por un mamparo longitudinal estanco, está lleno de agua de mar (1,025 ton./ m 3 ).

Calcular la escora que sufrirá si se vacía la mitad de un lateral de dicho tanque.

R.: 3o

13. Ejercicio No Calcule el valor de X para trimar la gabarra

R = 10 m.

14. Calcule el peso W2 para adrizar la gabarra.

R. = 160 ton.

15. Calcule W1 para neutralizar la escora y W2 para trimar la gabarra

R.= W1 = 140 ton. W2 = 67,5 ton.

Solución del escenario No 11

Un buque de 8153,75 ton. de desplazamiento tiene un KM de 8,00 m. y un KG de

7,50 m.

En el hay un doble fondo de 15 m. de eslora, 10 m. de ancho y 2 m. de alto que está lleno con agua de mar (1,025 ton./m3)

Hallar el nuevo GM si se deslastra 1 m.

•

Calculo de GG 1 :

Ton. descargadas = 15 m. x 10 m. x 1 m. x 1,025 ton./m 3 = 153,75 ton.

∆ f = ∆ i – lastre = 8.153,75 ton. – 153,75 ton. = 8.000 ton.

GG 1 = w x d/ ∆ f

153,75 x 6 m./ 8.000 ton. = 0,115 m.

• Calculo de G 1 G V :

G 1 G V = i/ ∆ x δ sw 15 m. x (10m.) 3 x 1,025 ton./m 3 / 12 x 8.000 ton. = 0,16 m.

• Calculo del GM:

GM i = KM i – KG i = 8,00 m. – 7,50 m. = 0,50 m.

G v M = GM i – (GG 1 + G 1 G v ) = 0,50 m. – (0,115 m. + 0,161 m.) = ↑ 0,224 m.

Resultado: GM v = 0,22 m.

Solución del escenario No 12

Un buque de 8.000 ton. de desplazamiento tiene un KM de 7,5 m . y un KG de 7,0 m.

Un tanque doble fondo de 12 m. de eslora, 15 m. de manga y 1 m. de puntal, dividido

en su sección media por un mamparo longitudinal estanco, está lleno de agua de mar

(1,025 ton./ m 3 ).

Calcular la escora que sufrirá si se vacía la mitad de un lateral de dicho tanque.

•

Calculo del peso descargado:

P desc . = 12 m. x 7,5 m. x 0,5 m. x 1,025 ton./ m3 = 46,125 ton.

•

Calculo de la elevación de G (GG 1 )

GG 1 = w x d / ∆ - w = 46,125 ton. x 6,25 m. / 8.000 ton. – 46,125 ton. = 0,037 m.

•

Calculo del desplazamiento lateral G (G 1 G 2 ):

G 1 G 2 = w x d / ∆ - w = 46,125 ton. x 3,75 m. / 8.000 ton. – 46,125 ton. = 0,022 m.

•

Calculo de la pérdida virtual de GM (G1Gv):

G 1 G v = i / ∆ f x δ sw = e x m 3 /12 x ∆ f x δ sw = 12 m. (7,5 m.) 3 / 12 x 7.953,87 ton. x 1,025

ton./ m 3 = 0,0544 m.

•

Calculo de G v M:

G v M = KM – KG i – (GG 1 + G 1 G v ) = 7,50 m. – 7,00 m. – (0,037 m. + 0,0544 m.) =

0,408 m.

•

Calculo de la escora:

Triangulo G v G 2 M => tang Ө =G 2 G v / G v M = 0,0227/ 0,408 =0,054 ≈ 3o

23Apuntes de Estabilidad

Solución del problema No 13

X . 35 ton. = 35 m. . 10 ton.

X = 350 ton./ 35 ton.

X = 10 m.

Solución del problema No 14

15 m. . W2 = 40 m. 60 ton.

W2 = 2400 tom./15 m.

W2 = 160 ton.

Solución del problema No 15

15 m. . W1 = 35 m. . 60 ton.

W1 = 2100 ton./15 m.

W1 = 140 ton.

40 m. . W2 = 45 m. . 60 ton.

W2 = 2700 ton./40 m.

W2 = 67,5 ton.

Bibliografía consultada[editar]

• Teoría del Buque, Cesáreo Díaz Fernández, Barcelona, 1972 B 43259 1972. Pág. 233 y 287.
• Elementos de Arquitectura Naval, Antonio MANDELLI. Librería editorial Alsina Buenos Aires 1986. ISBN 950-553-026-9.
• El Bulk Carrier en la Práctica,J.A.Bustabad, URMA, S.A. de Ediciones. Bilbao 1980 ISBN 84-314-0345-4.Págs 106/108.
• Convenio internacional para la seguridad de la vida humana en el mar, 1974 y su protocolo de 1988, SOLAS, OMI, ISBN 92-801-0091-2 Pag 68 y 69